Helpful tools for understanding nuclear fusion

This is the third post in our series on nuclear fusion power.

There are many proposed methods for creating fusion power plants. How can we discern which are the most practical? How can we tell which fuels will be the easiest to use?

The answers to these questions are rooted deeply in the underlying physics of fusion power, but here we can look at the high-level concepts that are useful for studying fusion power systems.

These are the concepts I found to be very useful and descriptive during my research into fusion power. If you read scientific literature on fusion, you are bound to run across these terms eventually. Unfortunately many scientists forgo defining these terms in their scientific works, assuming that their readers will already be familiar with them.

Ignition State

Ignition state occurs when enough fusion energy is being created in the fusion plasma that the amount of energy kept in the plasma is enough to continue causing the current rate of fusions. Another way to look at it is that there is enough energy kept in the plasma to maintain fusion conditions.

The analogy to other types of ‘ignition’ you may be familiar with is strong.  For example, it is analogous to burning a dry piece of paper. Once you have light one end, the burning paper provides enough energy to keep itself burning, and it quickly heats nearby areas and lights them on fire as well. In the case of fusion power, the ‘paper’ is our fusion plasma fuels, and the ‘combustion’ is nuclear fusion. This analogy is particularly apt since nuclear fusion conditions for earth-based reactors typically rely primarily on the temperature of the plasma, just as the temperature of the paper primarily dictates whether it will burst into flame.

The majority of the energy produced leaves the fusion plasma and strikes the sides of the reactor. This exiting energy is what we capture to produce electricity. The percentage of fusion energy contained in the plasma depends on both the fusion process and fusion technique that are implemented. It is important to keep in mind that only charged particles (such as electrons and ions) interact in a substantial way with the plasma, and they only leave a small percentage of their energy in the plasma, on average.

Ignition state need not be dangerous, there is no runaway reaction because energy output is entirely dependent on the input of fuel. Also, the total energy that can possibly be released by all fuel ions in the reaction chamber at once is not enough to be of threat to the structure of the reactor. This is different than with fission reactors, where there is technically enough fuel on the premises to cause a very substantial problem if something catastrophic happens to cause a runaway reaction.

If we can create a stable ignition state, we can simply feed in fuel in the right proportions to receive net energy output. Plasma in an ignited state would be emitting a tremendous amount of energy. We know this for a number of reasons:

1. Only a fraction of the energy emitted from most fusion processes (fuel cycles) is in the form of charged particles. Only charged particles will leave a large amount of energy in the plasma as they exit. Neutrons pretty much just fly right out and continue until they hit a large or very dense material (high-Z elements with many protons in their nucleus (such as lead) are useful for stopping neutrons).
2. Not all of the charged particle energy is left in the plasma. Much of it will exit the plasma because the particles are so energetic that the plasma containment will not stop them from exiting.
3. Bremsstrahlung losses for plasmas at these temperatures are quite high. Bremsstrahlung is a word that means ‘braking radiation’. It applies to rapidly accelerating or decelerating charged particles ( most notably electrons since they are so light). In plasmas that are hot enough to be in the ignition state, electrons are being accelerated around at incredible rates, leading to a lot of bremsstrahlung radiation. This radiation is in the form of electromagnetic waves (radio, x-ray, light, etc), so it tends to fly right out of the plasma.

All of these energy loss mechanisms mean that the plasma only gets a small fraction of the energy produced by fusions. The heating necessary to maintain fusion temperatures due to heat losses is often equivalent to several hundred megawatts. In the ignition state, the energy from fusions hitting the sides of the reactor would likely be several times that value.

In short, ignition state is one of the holy grails of fusion research. Ignition state means we can pretty much just feed in fuel ions and energy comes out. Certainly the containment field equipment will be working at full power, as will many other systems in the power plant. The point is that we will not have to apply extra heating to the plasma to keep it hot enough for fusions to continue. Ignition state means that we have a sustained chain reaction that is producing enough heat to keep itself going. All we need to do is keep it contained and feed it fuel.

Lawson Criterion

First described by John D. Lawson in 1957, it is a measure of the minimal conditions required for achieving ignition in a plasma. We can think of this value as the relative difficulty of achieving ignition of a fuel plasma.

The Lawson criterion is an inequality demonstrating that the product of electron density (η_e) and energy confinement time (Τ_E) must be greater than a quantity called ‘L’ in order for ignition to be possible. The value of L depends on a number of factors which we will go into shortly. For instance, at a temperature of 25 KeV, L has the following value for the D-T reaction (the deuterium-tritium fusion process):

This means that in order for an ignition state to happen, the product on the left has to be greater than the value on the right. The value on the right in this equation is L.

Here is an example of the L function, derived under a certain set of assumptions. For instance, this derivation assumes that the densities of the different ions are the same, and the temperatures of the electrons and ions are the same (although smeared in a Maxwellian fashion).

It is important to note that the value L is different for different temperatures. Reflecting the difference in energy confinement time and electron density necessary to achieve fusion at the given temperature level.

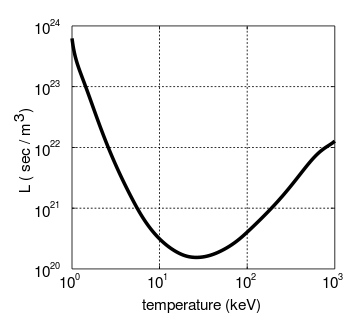
The temperature of interest with regards to the Lawson criterion is the minimum of the quantity L, which (as you can see above) depends on temperature and a number of other factors. What this minimum represents is a loose idea of what the minimal conditions are for fusion of this type. It is also informative about what the optimal temperature is for a given fusion process. Different fuels tend to require different temperatures for the minimization of their Lawson criterion. For example, one fuel might hit its minimum at 25 keV, and another might hit it at 50keV.

Never seen the “eV” unit before? It is an electron volt, a unit of energy that is very useful when studying nuclear interactions.

I have included a pdf version of my notes on this version of the derivation of the Lawson criterion. In brief, it is derived from equality of energy in (from fusion reactions) and energy out (such as particles hitting the walls, radiation, etc). The energy out mechanisms are all wrapped into the concept of energy confinement time, rather than being considered on an individual basis.

A picture is useful here, to illustrate how the L value changes with temperature. This picture is for D-T (the deuterium-tritium fusion process). As you can see, for D-T the L function has a minimum around 25 keV. This means that the conditions of fusion are most easily attained for D-T around a temperature of 25 KeV.

Fusion Performance Parameter

This quantity fulfills a role similar to the Lawson criterion, and has a similar derivation. It is the product of energy confinement time (τ_E) and plasma pressure (ρ). There are two possible ways to represent the fusion performance parameter: 1) in terms of plasma pressure 2) in terms of plasma Beta.

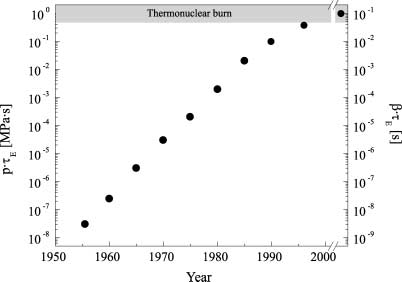
For D-T the fusion performance parameter must reach about 1MPa·s (mega pascal seconds) at a plasma temperature of 15KeV for ignition to occur.

On this graph you can see our progress towards ignition. The results from the 1990s are from the Joint European Torus (JET) and from the Japanese tokamak JT-60U. ITER is expected to reach ignition state. It is the upper right dot on the graph. What we can see here is that in the last several decades we have made demonstrated progress towards achieving fusion.

Energy Gain Factor

Energy Gain Factor is often referred to as ‘Q’. Q is defined as: power from fusion divided by the power of external heating required to keep fusion going.

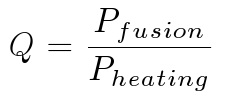
Energy Gain Factor is a measure of the energy released from fusion reactions compared with the external energy input required to create the conditions of fusion. JET achieved a Q of approximately 0.7. Ignition state corresponds to a Q value of infinity, since the reaction would require no external heating to continue.

Here I have demonstrated a way to break down the denominator in a more educational fashion. To do this, we used a number of assumptions.

Firstly, we assumed that the energy from charged particles stays in the plasma, and all neutron energy leaves the plasma. This assumption has some basis in fact, since neutrons generally do not interact with plasmas. If anything, this overestimates the amount of energy staying in the plasma, since it assumes that all of the charged particle energy stays. In a real reactor, some fraction of the energy in charged particles would leave the plasma and hit the outsides of the reactor. The fraction of energy from charged particles stays in plasma is given as f_ch.

Secondly, we assume that neutron energy is converted into heat, which is then turned into electricity with efficiency (η_elec). We use some fraction of this electricity to run reactor heating systems (f_recirc). We convert electricity to heat with some efficiency (η_heat). This heat is used to sustain the ignition condition.

Some rough estimates at these numbers leads to the following calculation for a Q factor for a commercial reactor. Assumptions for these numbers: This is for D-T, where 20% of energy is in charged particles. We would prefer to only recirculate a fifth of the electricity produced. Efficiency of converting heat to electricity is 0.4 reasonable considering our experience. Efficiency of converting electricity to plasma heat is 0.7.

According to Wikipedia’s article on fusion energy gain factor, this means that a commercial reactor seems to require a minimum Q between 15 and 22. ITER is expected to reach a Q value of 10, but steady state of only Q = 5. DEMO is planned to reach Q of 25 at a thermal power rating of 2GW steady-state. This is of course very ambitious. It is humbling to think that DEMO is not expected to be operating until at least the year 2033.

For further reading, we highly recommend the follow-up posts on the subject of

1. What fusion fuel cycles are, and how they work.
2. The basic realities of fusion reactor design.

That’s all for now folks! Stay tuned for further posts in the nuclear fusion series.